Given a positive integer n, generate an n x n matrix filled with elements from 1 to n^2 in spiral order.
Example 1:
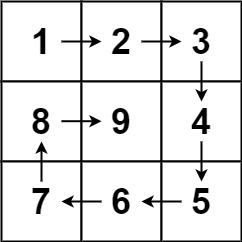
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]
Example 2:
Input: n = 1
Output: [[1]]
Constraints:
1 <= n <= 20
Understanding the Problem:
The problem statement asks for a function that, given a positive integer n, generates an n x n matrix filled with elements from 1 to n^2 in a spiral order. To tackle this problem efficiently, it's crucial to comprehend the nature of the spiral traversal within the matrix.
To identify recurring patterns, consider that any n x n square can be traversed in a circular manner, consisting of four sides: top, left, right, and bottom. The number of such circular traversals, or "loops," can be determined by n/2. For odd values of n, the middle number requires special handling.
For instance, in a 3 x 3 square:
# Given 3 * 3 Square, rotate in spiral order
- TOP
[0, 0] = 1; [0, 1] = 2;
- RIGHT
[0, 2] = 3; [1, 2] = 4;
- BOTTOM
[2, 2] = 5; [2, 1] = 6;
- LEFT
[2, 0] => 7; [1, 0] = 8;
- MIDDLE
[1, 1]
Finding the solution
The solution utilises the above understanding to systematically fill the matrix in a spiral order. By iteratively traversing the four sides of each loop and incrementally filling the matrix with integers, the algorithm constructs the desired spiral matrix efficiently.
const generateMatrix = function(n) {
let loop = Math.floor(n / 2);
let mid = Math.floor(n / 2);
let count = 1;
let offset = 1;
let x = 0;
let y = 0;
let result = new Array(n).fill(0).map(() => (new Array(n).fill(0)));
while (loop--) {
let col = y;
let row = x;
//TOP
for (; col < n - offset; col++) {
result[row][col] = count++;
};
//RIGHT
for (; row < n - offset; row++) {
result[row][col] = count++;
};
//BOTTOM
for (; col > y; col--) {
result[row][col] = count++;
};
//LEFT
for (; row > x; row--) {
result[row][col] = count++;
};
x++;
y++;
offset++;
}
if (n % 2 !== 0) {
result[mid][mid] = n * n;
};
return result;
}
Complexity analysis
Each of the four loops iterates n - offset times. The total number of loops is n/2.
Therefore, the worst-case time complexity of this solution is O(n^2).
Conclusion
In conclusion, the provided algorithm efficiently generates a spiral matrix by systematically traversing the matrix in a spiral order and filling it with consecutive integers. By understanding the underlying pattern of traversal and employing systematic loop operations, the algorithm achieves the desired functionality within a time complexity of O(n^2).

