Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

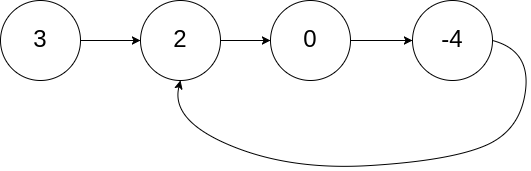
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

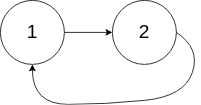
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 10<sup>4</sup>].

• -10<sup>5</sup> <= Node.val <= 10<sup>5</sup>

• pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Thinking process

If there is a cycle in a linked list, what happens when we traverse it? The indicator is when we return to a specific node that marks the beginning. This implies that if we can confirm encountering a node previously, a cycle exists; otherwise, there is no cycle in the linked list. So, how can we make sure if we've seen a node before?

A data structure like a HashSetcan assist in this scenario. By adding unseen nodes to the HashSet, we encounter two scenarios:

1. If no node has been seen before, there is no cycle.

2. If a node has been added to the HashSet, a cycle exists.

Approach using HashSet

1. Initialize a HashSet and set the current node to the head of the linked list.

2. Traverse through the linked list by moving the current node:

   • If the current node has not been added to the HashSet before, add it to the HashSet and move to the next node.

   • If the current node has been added to the HashSet before, return the current node.

3. If no cycle is found after traversing the entire linked list, return null.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function(head) {
    let hashset = new Set();
    let node = head;
    while (node) {
        if (hashset.has(node)) {
            return node;
        } else {
            hashset.add(node);
            node = node.next;
            }
    }
    return null;
}

Time & Space Complexity Analysis

Time Complexity Analysis:

Traversing through the linked list takes O(n) time, where n is the number of nodes in the linked list. - Adding each node to the HashSet or checking for its existence in the HashSet takes O(1) time. - Therefore, the overall time complexity is O(n).

Space Complexity Analysis: The space complexity is O(n) since we need additional space to store visited nodes in the HashSet, where n is the number of nodes in the linked list.